Skip to main content

Resolution

Chứng minh phản chứng

  1. Negate the conclusion trying to be proven(!)
  2. Then turn this into CNF
  3. Attempt to derive empty clause
  4. If found this indicates the set of clauses was not satisfiable
  5. This then means that the original conclusion was supported by the clauses

→ Everything separate by ∧ is a fact​

Examples​

Ex1​

∀𝑥 433Inst(x) → Cool(x)
433Inst(Jon)
Prove Cool(Jon)

Solution​

→  433Inst(x) → Cool(x) ∧ 433Inst(Jon) ∧ ¬ Cool(Jon) **
→  (¬433Inst(x) V Cool(x)) ∧ 433Inst(Jon) ∧ ¬ Cool(Jon)
→  mgu(x → Jon) we get (¬433Inst(Jon) V Cool(Jon))
For ** to be true ¬433Inst(Jon) V Cool(Jon) need to be true
→ Cool(Jon) need to be true
→ (¬433Inst(x) V Cool(x)) ∧ 433Inst(Jon) ∧ (¬Cool(Jon)) ∧ (Cool(Jon))

We have contradiction since (¬Cool(Jon)) ∧ (Cool(Jon)) resolve to empty clause

Facts​

alt text

Extension Rules​

Knowledge on top creates knowledge at the bottom

alt text

Resolution rule​

example 1​

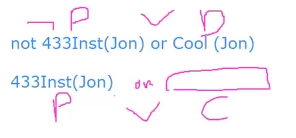
Can always use empty clause as one of the thing needed in the formula alt text alt text

C doesnt exist → only D

Actually we dont have Jon in all clauses, they are x:
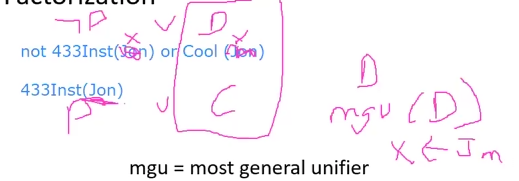
→ mgu(x <- Jon) alt text

example 2​

alt text

Factorization​

If I have a bunch of V and some of them are P and P'. P' is a variant of P (same but applied to different predicate letter like P(x) and P(y) or P(a) and P(b)) we can drop P'

Examples

Ex1​

1. 𝑝 ∨ 𝑞
2. 𝑝 ∨ ¬𝑞
3. ¬𝑝 ∨ 𝑞, 
4. ¬𝑝 ∨ ¬𝑞
5. p ∨ p resolve (1) and (2)
6. p factorize (5)
7. ¬𝑝 ∨ ¬𝑝 resolve (3) and (4)
8. ¬𝑝 factorize (7)
9. ∎ resolve (6) and (8)

Ex2​

1. 𝑃(𝑥) ∨ 𝑅(𝑥) 
2. ¬𝑅(𝑓(𝑎, 𝑏))
3. ¬𝑃(g(𝑎, 𝑏))
4. mgu = {x ≈ f(a, b)} → 𝑃(f(a, b)) ∨ 𝑅(𝑓(𝑎, 𝑏)) ∧ ¬𝑅(𝑓(𝑎, 𝑏)) 
→ 𝑃(f(a, b)) by resolution
5. mgu = {x ≈ f(a, b), x ≈ g(𝑎, 𝑏)} → R(g(a, b))
Cant reach empty clause

Ex3​

1. 𝑃(𝑥) ∨ 𝑅(𝑦) 
2. ¬𝑅(𝑓(𝑎, 𝑏))
3. ¬𝑃(g(𝑎, 𝑏))
4. P(x) resolve (1) and (2) with mgu = {y ≈ f(a, b)}
5. ∎ resolve (3) and (4) with mgu = {x ≈ g(a, b)}