Skip to main content

And Tree

Pros​

  • Good for optimization problems
  • Good for exhaustive search
  • Tree can be bounded (get rid of redundant branches)
  • Good for problems where you need to solve all sub-problems and combine them

Cons​

  • Take a lot of space and computation

Model​

A = (S, T)

Prob​

set that contains all of the possible versions of the problem I can have

ex Scheduling problem​

  • Empty sechdule
  • One thing is scheduled
  • Different complete schedules These things are subversion of prob and within prob

Div​

is a relationship on which version of prob can be divided into other version of prob

→ First we define what are all the possible ver of the problem
Div says if I have this ver of prob, this is what it can turn into

example​

  • given an empty schedule
  • Div assigns one thing

or

  • given one game which can be put in 15 different slot
  • Div goes and put it in all those possible slots → it defines that one thing can turn into 15 different things

basically

  • for the city problem, Prob is all the cities. Prob+ is any city could go to any other cities. Div says no just the one with roads matter.

State S​

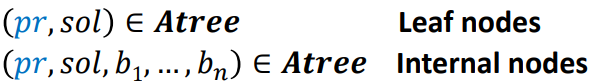
Every S is an And tree alt text or alt text

example​

alt text

Transitions​

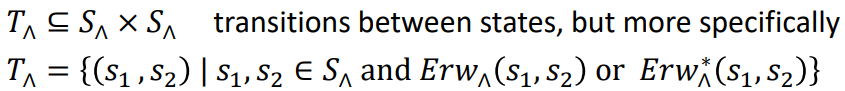
We can expand or backtrack the tree alt text alt text

→ Div and Prob provide S and T​

Extension function​

alt text

second point​

alt text

third point​

Modification of an internal node:

  • Take the pointed node & put something different in. alt text

Backtracking​

Define a critical point to undo

Process​

P = (A, Env, K)

K takes a state or a transition in this case means taking a leaf node and do sth with it

→ need a function to pick a leaf node and a function to do sth w it​

fleaf value all the leaf nodes and select one​

ftrans selects on transitions from Div to deal w the selected leaf​

Normally, we solved the most constraint / problematic ones first since the other are more flexible

Ins​

Ins = (s0, G)​

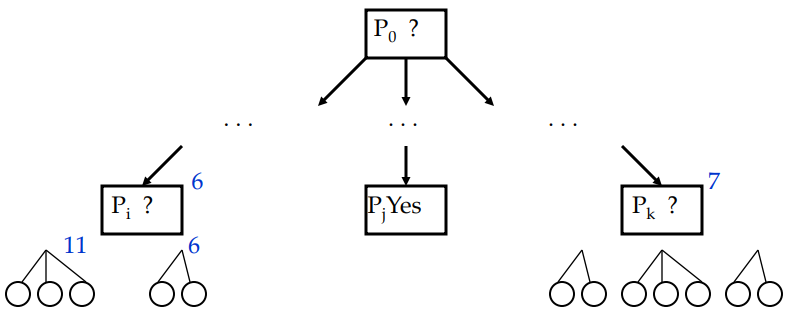
alt text alt text

Fringe​

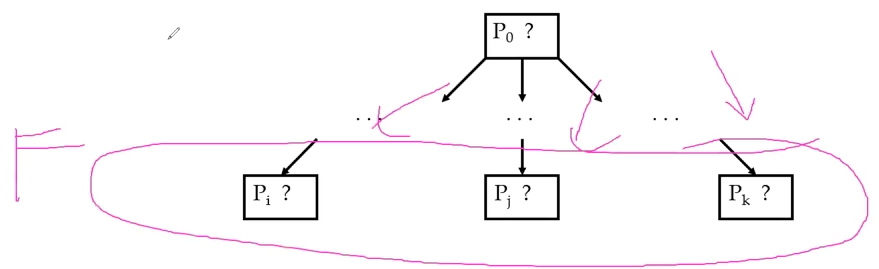
there are 3 leaf nodes in this fringe alt text

Example​

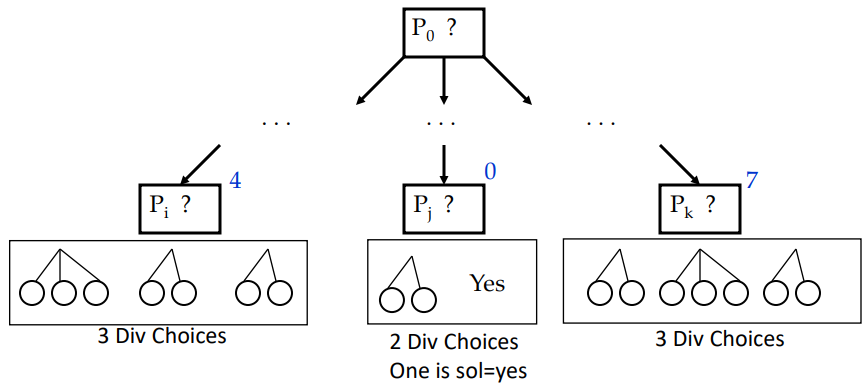
alt text

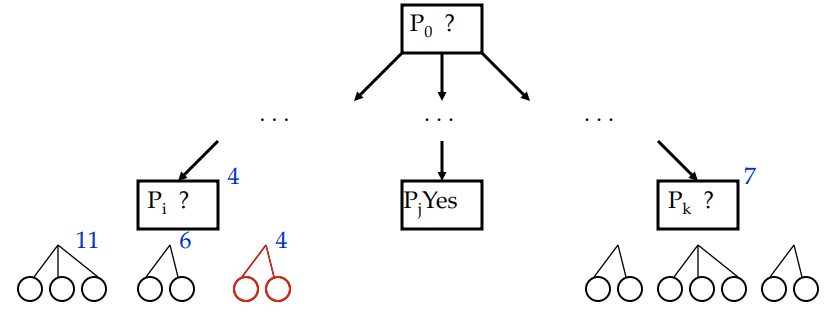
Tree prefers solved node → Pj = Yes. Then, expand the next min val one which is 4 alt text

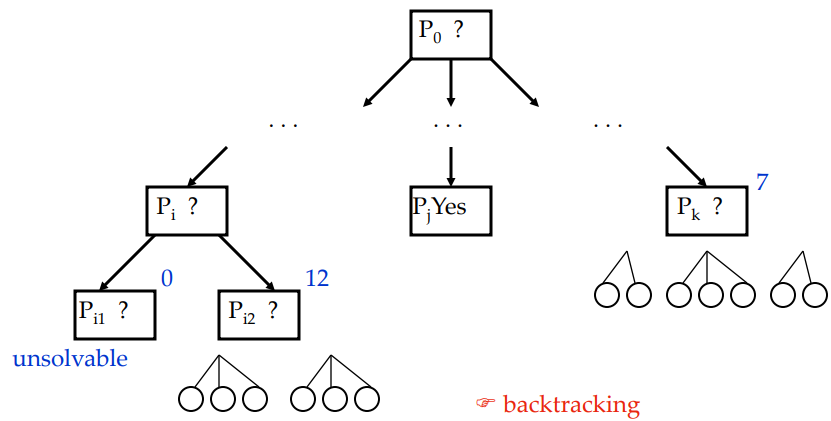
Now 4 has two options under it, the new fringe contains that two and Pk alt text

Now if a leaf node require backtracking (unsolvable in this case), prefer to deal with it first. Backtrack to option 6 alt text alt text

Design AndTree Model​

  1. How do I present my problem → Prob
  2. Identify how a problem is solved
  3. Identify how to divide problem into subproblems → Div
  4. Determine if its possible to run into deadends and how to deal with it (backtracking?)

Design AndTree Process​

  1. How to value the problems (leaf)?
  • Prioritize solved problem → fleaf
  1. Use ftrans to pick transition
  • If unsovable, backtrack
  • If can be solved, do it
  • If something isnt done, evaluate transitions and pick one