Skip to main content

Unification

attempt to find the most general unifier (mgu)

mgu is a valid mapping of variable/constant/function mapping to make two terms the same

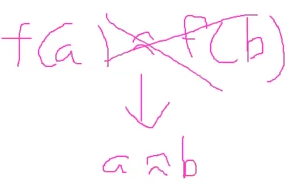
Ex. if I have f(a) and f(x)
• mgu mapping x->a makes f(a)=f(a)

alt text

these terms will be in a set {}. Each term means these can be unified together, they can exist at the same time or be replaceable one with the other.

alt text

which means you cant unified these terms

Extension Rules​

Delete​

alt text

Decompose​

alt text

ex​

alt text

alt text

Orient​

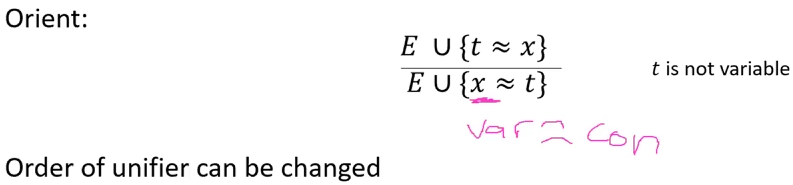
We prefer var replaced by con alt text

Substitute​

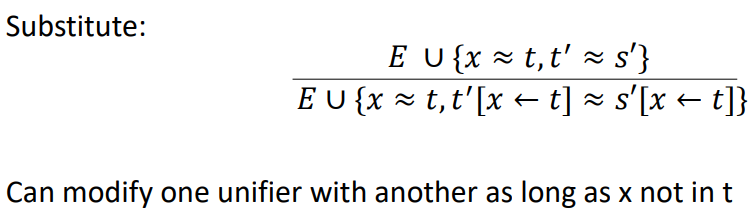
alt text

ex​

alt text

as long as x not in t​

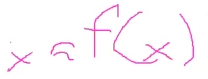
alt text

Occurs​

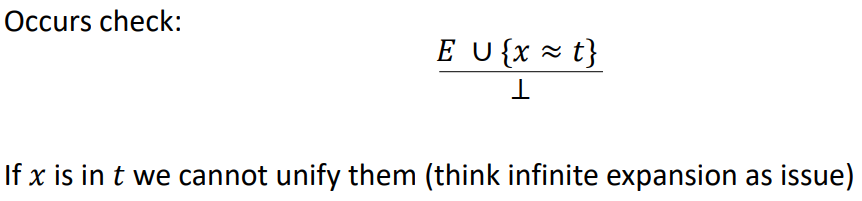
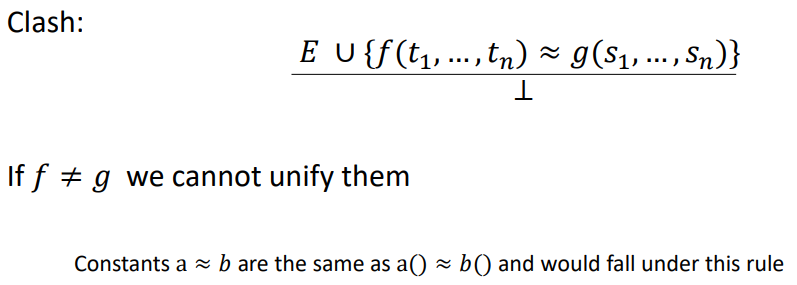
alt text

ex​

alt text

Clash​

alt text

ex​

alt text

Summary​

  • Success: no more rules left
  • Failure: Occur check or Substitute are not applicable: ⊥ alt text

Examples

Example 1​

𝑓(g(𝑥, 𝑦), 𝑐) ≈ 𝑓(g(𝑓(𝑑, 𝑥), 𝑧), 𝑐) 
decompose: 
{g(x, y) ≈ g(𝑓(𝑑, 𝑥), 𝑧), c ≈ c}  → two facts created by decomposition 
delete:
{g(x, y) ≈ g(𝑓(𝑑, 𝑥), 𝑧)}
decompose
{x ≈ f(d, x), y ≈ z}
occur check ⊥

Example 2​

ℎ(𝑐, 𝑑, g(𝑥, 𝑦)) ≈ ℎ(𝑧, 𝑑, g(g(𝑎, 𝑦), 𝑧))
decompose
{c ≈ z, d ≈ d, g(x, y) ≈ g(g(𝑎, 𝑦), 𝑧)}
delete
{c ≈ z, g(x, y) ≈ g(g(𝑎, 𝑦), 𝑧)}
orient
{z ≈ c, g(x, y) ≈ g(g(𝑎, 𝑦), 𝑧)}
decompose
{z ≈ c, x ≈ g(𝑎, 𝑦), y ≈ 𝑧}
substitute
{z ≈ c, x ≈ g(𝑎, 𝑦), y ≈ c}
substitute
{z ≈ c, x ≈ g(𝑎, c), y ≈ c}
done
mgu = {z ≈ c, x ≈ g(𝑎, c), y ≈ c}